Der Auftrieb - ein simples Modell zur Erklärung

1. Einführung
2. Anordnung
3. Wesentliche Gedankengänge zur Vorbereitung
4. Zu Staudruck und Staupunkt
5. Beobachtung im Kanal
6. Gedankliche Vorgaben und die Abgrenzung zu verbreiteten Erklärungsversuchen
7. Simples Erklärungsmodell
8. Zusammenfassung
9. Nachtrag für eine genauere Rechnung
10. Zirkulation in Theorie und Beobachtung
11. Kann man diesen Ansatz in der Schule überprüfen?
12. Eine technische Anmerkung
13. Dokumentation der Änderungen

1. Einführung

Für den Unterricht an der Schule entsteht immer wieder das Problem, eine quantitative Erklärung für den dynamischen Auftrieb zu finden. Darüber gibt es einen mit Hingabe geführten Streit im Bereich der Didaktik^*)der Physik; auch aktuelle Ausgaben von Schulbüchern verbreiten leider unverändert Vermutungen zum Auftrieb, die keiner Nachprüfung standhalten.
Das nachfolgende Modell ist ein Lösungsangebot,das außerordentlich simpel argumentiert, aber auf dem physikalisch korrekten Hintergrund aufbaut, der in jedem kleinen Wasser- oder Windkanal überprüft werden kann. Das Verständnis der einfachen Erklärung setzt die Kenntnis der Phänomene in Zusammenhang mit der Bernoullischen Gleichung voraus, die Druck und Geschwindigkeit in Beziehung setzt; in der Sekundarstufe II kann das Modell auch quantitativ erarbeitet werden.
Die strittigen Diskussionspunkte der theoretischen Begründung tauchen darin gar nicht erst auf, weil nur die Beobachtung im Wind- oder Wasserkanal Ausgangspunkt der Erklärung ist. Für die Sekundarstufe I  ist dieses Modell nach unserer Auffassung auf jeden Fall eine hinreichende Grundlage. Die Erklärung ist in zwei Bildern zusammengefasst, die auch als PDF Dokument kopiert werden können:

Simple Erklärung des Auftriebs  Zwei Bilder mit der Zusammenfassung der nachfolgenden Erklärung (PDF, 100 kByte). Das Bildmaterial mit dem Wasserkanal ist noch nicht perfekt, aber wir bemühen uns um besseres Bildmaterial in der nächsten Zeit. Versuche an der Schule werden in der Regel nicht sehr viele bessere Ergebnisse hervorbringen. Diese ganze Seite liegt ebenfalls als PDF Dokument vor (550 kByte).
*) Siehe dazu auch Literatur (Flugphysik) von Frau Prof. Rita Wodzinski  ( Didaktik an der GH Kassel).
 

2. Anordnung
Das nachstehende Bild 1a ist der Querschnitt durch einen rechteckigen Wind- oder Wasserkanal der Breite B und der Höhe H . Bei der Geschwindigkeit u ₀ ist die Durchflussmenge Q = B H u ₀[m³/s]. Die Breite B in Spannweitenrichtung y ist aus methodischen Gründen hinzugefügt, um mit Q die richtige Dimension für einen Volumenstrom zu haben. Im Kanal befindet sich eine Tragfläche, die eine dünne ebene Platte sein kann oder ein symmetrisches Profil.Wenn die Tragfläche keinen Anstellwinkel hat, entsteht auch kein Auftrieb. Die Tragfläche mit der Profiltiefe l befinde sich genau in der Mitte des Kanals, der die Höhe H = 2 l habe. Mit diesen - experimentell auch vernünftigen und gerechtfertigten - Abmessungenvereinfacht sich die nachfolgende theoretische Betrachtung. Die Drehachse des Profils sei aus Gründen der Symmetrie genau bei l /2 gelegen. Gezeichnet sind zwei benachbarte Partikel, die an der Tragfläche genau auf der Ober- und auf der Unterseite vorbei streichen.

Bild 1a. Geometriedes Strömungskanals.

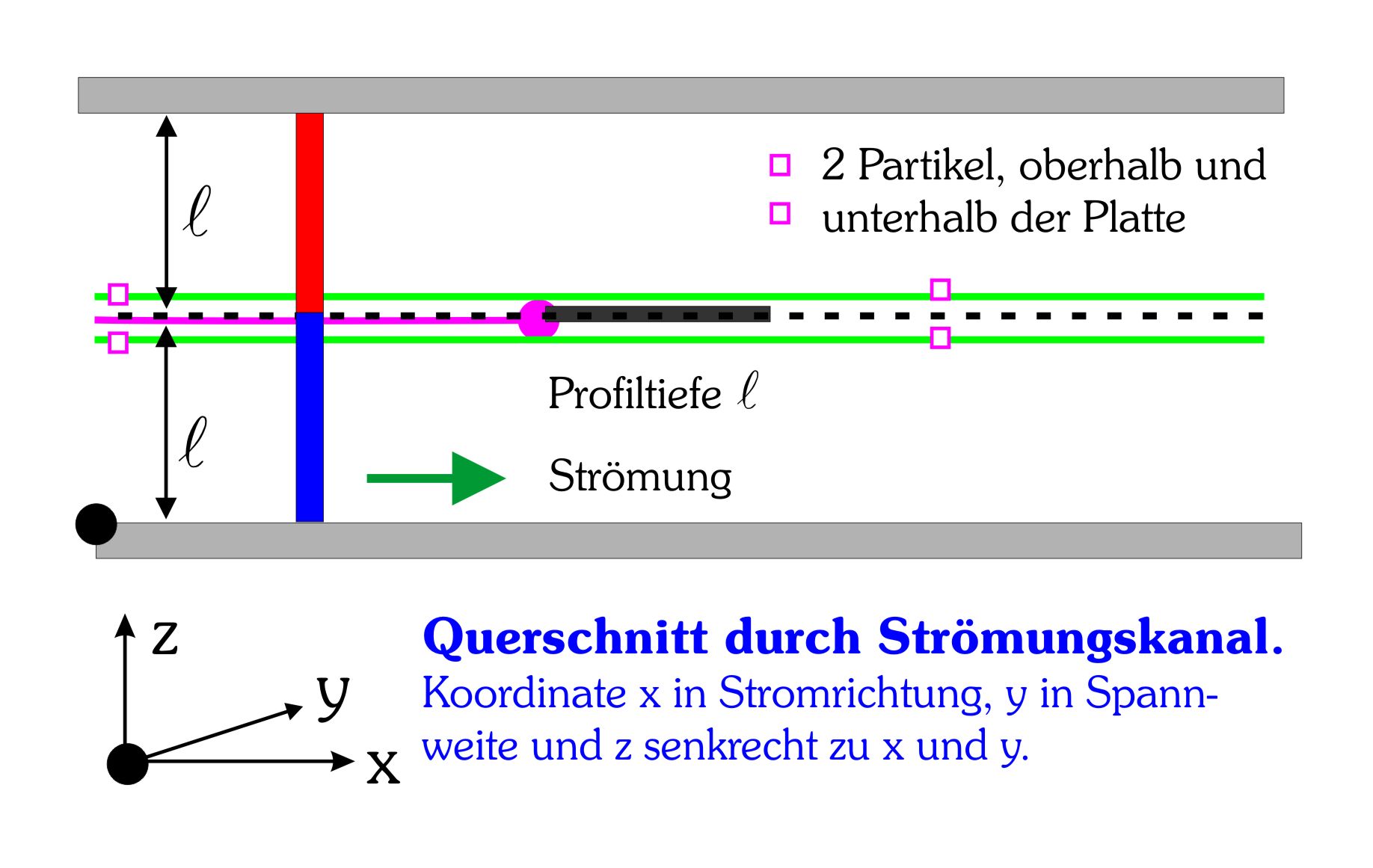
Warum ein Kanal? Es ist sicher anschaulicher,die Tragfläche gegenüber der ruhenden Luft zu bewegen, wie dies bei Lebewesen und Flugzeugen geschieht (oder in einer Versuchsanordnung wie dem Rundlauf ANIPROP RL3). Mit der Bewegung gegenüber der ruhendenLuft sollte eine Unterrichtseinheit "Physik des Fliegens" auch immer beginnen (siehe dazu " Auftrieb und Wirbeldichte beim Fliegen"). Der dynamische Auftrieb entsteht aber immer, wenn sich eine Strömung relativ zur Tragfläche bewegt. Man kann deshalb auch die Tragfläche an einem Ort ruhen lassen und die Strömung in Bewegung versetzen, was in einem Strömungskanal geschieht. Nachfolgend wird die Strömung durch Kanalwände begrenzt (geschlossener Kanal). Bei vielen einfachen Versuchsanordnungen mit Luft als Strömungsmedium wird nur die Luft angesaugt und beschleunigt; sie tritt als freier Luftstrahl aus, der für Strömungsexperimente verwendet wird (offener "Kanal"mit zwangsläufig unscharf begrenzten Rändern). Die Messergebnisse für den Antrieb unterscheiden sich zwar je nach Versuchsanordnung geringfügig, aber der physikalische Effekt der starken Querkraft (eben der dynamische Auftrieb) beruht beim freien Flug und im offenen oder geschlossenen Messkanal auf den gleichen strömungsmechanischen Grundlagen.
Luft oder Wasser unterscheiden sich bei kleinen Geschwindigkeiten nicht in ihrer Fähigkeit, dynamischen Auftrieb zu erzeugen. Wegen der größeren Dichte ist die Auftriebskraft in Wasser entsprechend viel größer, allerdings sind die Strömungsgeschwindigkeiten in Wasser vergleichsweise niedriger.
Dicke Tragfläche. Bei einer endlich dicken Tragfläche stellt sich schon ohne Anstellwinkel auf Ober- und Unterseite eine symmetrische Druckverteilung ein, die auf beiden Seiten durch Unterdruck gekennzeichnet ist. Die Ursache ist die Verdrängung der Strömung.
 

3. Wesentliche Gedankengänge zur Vorbereitung

• Der ankommende Volumenstrom Q soll bei allen Überlegungen konstant sein.

• Wenn sich der Querschnitt eines festen Volumenstroms Q verengt, dann erhöht sich zwangsläufig die örtliche Fließgeschwindigkeit. Größere Fließgeschwindigkeit bedeutet, dass der Druck in der Strömung abnimmt (was mit dem Standardexperiment der Strömung in einem Glasrohr mit verschiedenen Querschnitten gezeigt wird). Umgekehrt nimmt die Geschwindigkeit ab, wenn sich der Querschnitt weitet. Dann vergrößert sich der Druck.

Zusätzliche quantitative Aussagen:

• Der Druck in der ankommenden Strömung mit der Geschwindigkeit u ₀ soll p ₀ sein (Eintrittsort am linken Kanalrand).

• Die Bernoullische Gleichung stellt einen Zusammenhang her zwischen dem örtlichen Druck p ₁ und der örtlichen Fließgeschwindigkeit u ₁ (an einer beliebigen Stelle im Kanal) im Vergleich zu den Verhältnissen in der Anströmung:  p ₀+ 1/2 rho u ₀²= p ₁+ 1/2 rho u ₁².

• Die Dichte des strömenden Mediums (Luft oder Wasser) sei "rho" . Die kinetische Energie der Strömung am Eintrittsort, bezogen auf die Volumeneinheit, heisst auch Staudruck q ₀= 1/2 rho u ₀². Ist die Geschwindigkeit am Ort "1" bekannt, dann kann aus der Bernoullischen Gleichung auch der dortige Druck berechnet werden.

4. Zu Staudruck und Staupunkt
Die Größe q ₀ ist zunächst einmal die kinetische Energie eines kleinen Massenelementes dM in der Strömung (1/2 M u ₀²), bezogen auf das von ihm eingenommene Volumen dV . Es ist rho = dM/dV . Da Energie/Volumen die gleiche Dimension hat wie Kraft/Fläche, motiviert dies die Einführung von q ₀ als Referenzgröße für Drücke in der Strömung.Die Bezeichnung Staudruck leitet sich aus folgender Tatsache ab:Der Staudruck herrscht als Überdruck gegenüber dem Ruhedruck p ₀ in der Anströmung im sogenannten Staupunkt , in dem sich dieStrömung an der angeströmten Tragfläche verzweigt. Genau im Staupunkt ist die Geschwindigkeit u ₁ der Strömung null. Das Strömungspartikel, das genau auf den Staupunkt zufließt, kommt also eigentlich nie im Staupunkt an. Tatsächlich hat die Strömung immer eine natürliche Unruhe (Fluktuation), so dass dieser Gedankengang nur eine rechnerische Spielerei ist. Der Staupunktist nur im zweidimensionalen Querschnitt durch eine Flügelumströmung wirklich ein Punkt. Bei einem Tragflügel mit seiner Ausdehnung in Spannweite hat jeder Querschnitt seinen Staupunkt. Schaut man unter die angeströmte Tragfläche, dann verzweigt sich die Strömung über die ganze Spannweite und der Staupunkt ist tatsächlich eine Staulinie.
Anmerkung: Die im Deutschen übliche Bezeichnung Staudruck ist nicht besondersglücklich gewählt. Die im Englischen gebräuchliche Bezeichnung dynamic pressure kommt der physikalischen Herkunft dieser Größe nach dem Empfinden des Autors dieser Zeilen (W. Send) deutlich näher. 5. Beobachtung im Kanal
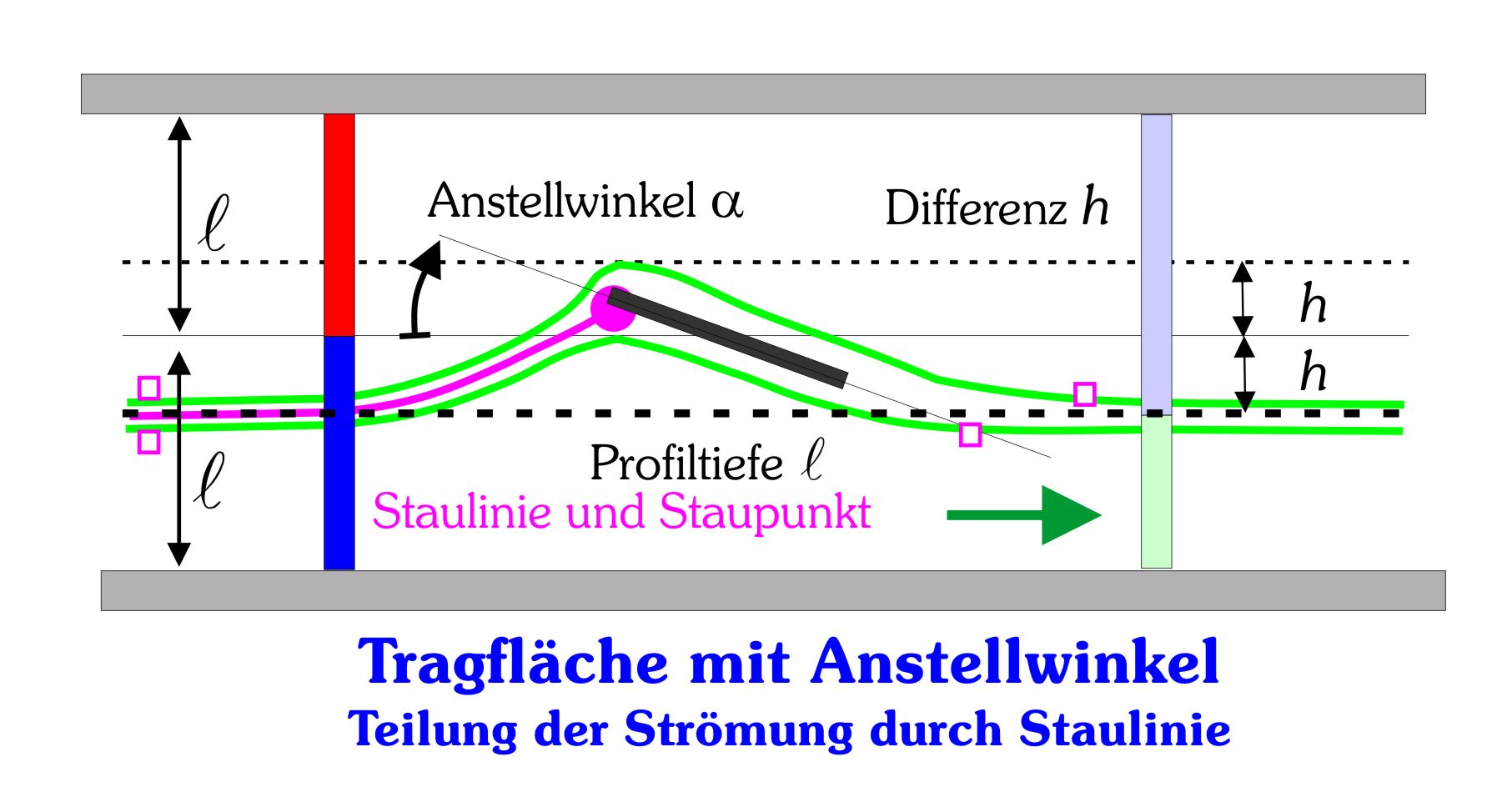
Wir beobachten zwei Partikel am Eintritt in die Messstrecke, die genau oberhalb und unterhalb der Tragfläche entlang fließen. Ohne Anstellwinkel treffen sich die beiden Partikel, die an der Stelle z = l in den Kanal eintreten, hinter der Tragfläche  wieder an gleicher Position in x -Richtung. Verändern wir den Anstellwinkel, so zeigt die Messung der Querkraft senkrecht zur Anströmung einen ansteigenden Wert, wenn der Anstellwinkel - wie gezeichnet - positiv erändert wird. Die Messung der Querkraft kann durch eine geeignete Messeinrichtung vorgenommen werden, auf die hier nicht weiter eingegangen sei.

• Zwei benachbarte Partikel, die weiterhin direkt oberhalb und unterhalb der Tragfläche strömen, haben mit steigendem Anstellwinkel einen tieferen Eintrittsort z , der als z = l-h bezeichnet ist. Die Absenkung h gegenüber der Mittellinie z=l ist geometrisch ungefähr durch die Lage der Hinterkante des Profils gekennzeichnet.

• Zwei Partikel, die vor der Tragfläche gleichzeitig starten, treffen sich nicht mehr hinter der Tragfläche. Das Partikel, das die Tragfläche unterhalb des Profils umströmt, trifft an einem festen Ort hinter der Tragfläche später ein als das oberhalb der Tragfläche vorbeistreichende Partikel.

• Die "teilende Stromlinie" zwischen den beiden betrachteten Partikeln endet in einem Staupunkt auf der Unterseite derTragfläche, in dem sich das gesamte Strömungsfeld verzweigt. An der Hinterkante beobachtet man einen solchen Staupunkt nicht, da dort die Partikel "glatt" abfließen und nicht in einem scharfen Bogen- wie an der Vorderkante - auf die Oberseite zurück strömen. Diese Tatsache ist Folge der geringen Zähigkeit in Wasser wie in Luft, ohne die Auftrieb nicht entstehen kann.

• Die Beobachtung sollte zeigen, dass die beiden Partikel mit der Bahn längs Ober- und Unterseite auf etwa der gleichen Höhe z=l-h die Messstrecke verlasssen, auf der sie eingetreten sind.

Jedenfalls ist diese letzte Feststellung das Ergebnis der theoretischen Rechnung für die zweidimensionale Umströmung eines Profils. Es find keine großräumige Ablenkung der Strömung als Folge des Auftriebs statt, wie dies immer wieder in Abhandlungen als Behauptung zu finden ist. Eine solche Behauptung hält keiner theoretischen Nachrechnung stand. Eine solche "zweidimensionale" Strömung lässt sich näherungsweise in einem Strömungskanal herstellen. Sie tritt aber auch auf in der Mitte langgestreckter Tragflächen, zum Beispiel bei Segelflugzeugen. Den Auftrieb in einem solchen "Mittelschnitt" ist in guter Näherung durch eine zweidimensionale Strömung - das ist mit Profilströmung gemeint -  zu beschreiben.

Realisiert werden kann die Beobachtung der Bahn einzelner Partikel durch impulsförmiges Einbringen von kleinen Bläschen oder Tinte bzw. Rauch in die Strömung. Die maximale vertikale Abweichung  h (gegenüber dem Eintrittsort ohne Anstellwinkel)  des oberhalb vorbei streichenden Partikels ist näherungsweise durch die geometrische Lage der Vorderkante bestimmt, die mit Anstellwinkel die vertikale Position l+h hat.

Man darf sich nicht der Vermutung hingeben, dass alle diese "Beobachtungen" ohne größeren experimentellen Aufwand auch auf leichte Weise gezeigt werden können. Der Rückgriff auf Bilder von Experimenten ist sinnvoll, aber nicht der Rückgriff auf beliebige grafische Darstellungen in Lehrbüchern! Dort steckt ja gerade das eingangs skizzierte Problem.

6. Gedankliche Vorgaben und die Abgrenzung zu verbreiteten Erklärungsversuchen

• Das Durchdenken der Entstehung des Auftriebs in einem Kanal lässt gar nicht erst den - physikalisch falschen und abwegigen -  Gedanken entstehen, die Quelle des Auftriebs könnte eine Art Rückstoßeffekt der Partikel auf der Unterseite der Tragfläche sein.

• Tatsächlich zeigt eine genauere Nachmessung (etwa durch kleine Bohröffnungen auf Ober- und Unterseite von der Vorderkante bis zur Hinterkante), dass der wesentliche Anteil des Auftriebs durch die Sogwirkung der Strömung auf der Oberseite des Profils entsteht. Der größere Anteil des Auftriebs kann also schon faktisch nicht durch ein solches Rückstoßargument begründet werden.
   
• Auch die Frage einer großräumigen Ablenkung der Strömung hinter der Tragfläche stellt sich nicht, weil der Auftrieb auch ohne diese Ablenkung vorhanden ist. Der häufig bemühte Randwirbel, zu dessen Ablenkung nach unten sich der Auftrieb als Reaktionskraft angeblich einstellen soll, ist ebenso wenig zur Erklärung erforderlich. Es ist zwar richtig, dass die beiden Randwirbel hinter den Flügelspitzen eines Flugzeug sich gegenseitig so beeinflussen, dass sie sich in einem freien Raum gegenseitig nach unten ziehen. In einer Kanalströmung bleiben sie aber praktisch horizontal hinter der Tragfläche und der Auftrieb entsteht gleichwohl.

• Die ausgeprägte Umströmung der Vorderkante mit der Folge eines starken Unterdrucks auf der Oberseite und entsprechendem Überdruck auf der Unterseite ist ein wesentlicher Punkt. Der Schwerpunkt der Druckverteilung liegt schon bei etwa einem Viertel der Flügeltiefe hinter der Vorderkante! Eine Strömung, die Auftrieb erzeugt, ist an Vorder- und Hinterkante extrem unsymmetrisch. Diese Unsymmetrie offenbart sich im glatten Abfluss an der Hinterkante, dessen Ursache wiederum die geringe Zähigkeit sowohl von Wasser wie von Luft ist. Man kann Strömungen erzeugen, die diesen glatten Abfluss nicht mehr haben, sondern die die Hinterkante umströmen. Dann entsteht wegen der Symmetrie auch kein Auftrieb mehr.

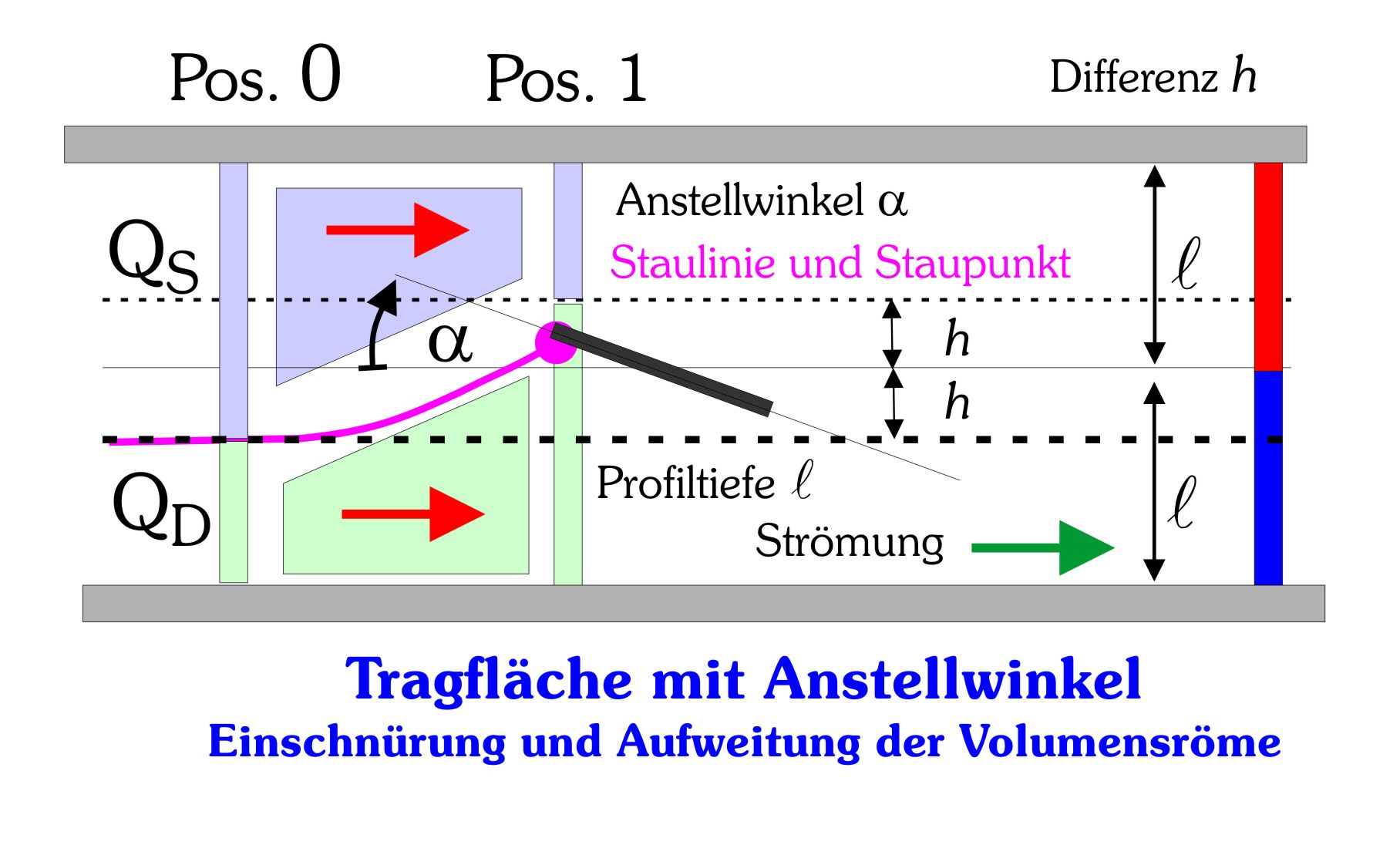
Bild 3. Einschnürungder anteiligen Volumenströme.
7. Simples Erklärungsmodell
Das Modell betrachtet die Volumenströme bei gegebenem Anstellwinkel alfa . Gegenüber der Strömung ohne Anstellwinkel fließt im Kanal die Menge Q_S= B (l+h) u ₀ auf der Oberseite des Profils vorbei, die Menge Q_D = B (l-h) u ₀ auf der Unterseite (Position 0). Im Bereich der Einschnürung der Strömung an der Position 1 gilt mit den einfachen geometrischen Näherungen für die Strömungsverhältnisse:

Q_S = B (l+h) u ₀ = B (l-h) u _1S
Q_D = B (l-h) u ₀ = B (l+h) u _1D

Wir nehmen nun an, dass die beiden Geschwindigkeiten u _1Sund u _1D in grober Näherung das Verhalten der Strömung auf der Oberseite (Saugseite, Index S) und der Unterseite (Druckseite, Index D) beschreiben. Das Verhalten der Strömung bei einer genauen Lösung des Problems (siehe " Profil im Windkanal") ist etwas komplizierter: Die Strömungsgeschwindigkeit nimmt von der Vorderkante zur Hinterkante ab, ebenso mit wachsender Entfernung von der Oberseite in Richtung Kanalwand. Analoges gilt für die Unterseite. Beide Abweichungen sind aber nur gradueller Art, nicht prinzipieller Natur. Schon bei einem Viertel der Flügeltiefe ist die Hälfte des Auftriebs aufgebaut, der sich bei einer genauen Lösung des Problems einstellt.

Für die Auftriebskraft F _A gilt, dass sie proportional zur Grundrissfläche S = B l und zum Staudruck q ₀ ist.  Die Proportionalitätskonstante heisst Auftriebsbeiwert c _A:

F _A = c _A   q ₀ S

Die Auftriebskraft ist die Differenz der Kräfte der Strömung auf der Druckseite und der Saugseite. Kraft ist Druck x Fläche , wobei der Druck sich aus der BernoullischenGleichung ergibt:

p _1S = p ₀ + 1/2 rho u ₀² -  1/2 rho u _1S²
p _1D = p ₀ + 1/2 rho u ₀² -  1/2 rho u _1D²

Mit u _1S = (l+h)/(l-h) u ₀ und u _1D = (l-h)/(l+h) u ₀ und  h/l = x folgen zunächst
u _1S = ( 1 +x)/( 1 -x) u ₀und u _1D = ( 1 -x)/( 1 +x)u ₀. Daraus mit
  F _A = c _A   q ₀ S = (p _1D - p _1S) S, und als Resultat

  F _A = [(1+x²) 8x]/[1-2x²+x⁴] q ₀ S,   =>  F _A = (8 x + ... ) q ₀ S

Die Beziehung wird deswegen so übersichtlich, weil konstante Geschwindigkeiten angenommen worden sind.  Die Ausrechnung aus den voranstehenden Geschwindigkeiten ergibt sich in wenigen Schritten. Da x = h/l = 1/2 sin( alfa ) nach den getroffenen Annahmengerade die Einschnürung bzw. Aufweitung der Strömung im Bereich der Vorderkante ist, ergibt sich für kleine Winkel der Auftriebsbeiwert

c _A = 8 x + ... = 4 sin (alfa) + ... (kleine Terme höherer Ordnung).

Die genaue Lösung für den Auftriebsbeiwert und vergleichbaren Strömungsbedingungen ergibt den Auftriebsbeiwert c_A   = 2pi sin (alfa), also auch quantitativ einen durchaus vergleichbaren Wert.

8. Zusammenfassung
Das einfache Ergebnis ist ein Resultat der einfachen geometrischen Verhältnisse, nämlich Kanalhöhe gleich doppelte Flügeltiefe. Für das Verständnis der Entstehung des Auftriebs ist dies aus unserer Sicht aber unerheblich. Wichtig ist die Verwendung einfacher geometrischer Verhältnisse und nachvollziehbarer physikalischer Überlegungen, um eine quantitative Aussage zur Auftriebskraftt reffen zu können.
 

Vertiefender Hinweis für Leserinnen und Leser mit physikalisch-theoretischem Hintergrundwissen. Entscheidend für das Ergebnis dieser vergleichsweise einfachen Überlegung ist, dass sie auf dem richtigen Weg einer physikalisch korrekten Behandlungder Fragestellung nach dem Druckbeiwert liegt. Tatsächlich erzielt man ein ähnliches Ergebnis, wenn man den Ansatz für eine approximative Lösung der Wirbeltransportgleichung betrachtet. Diese Gleichung folgt direkt aus dem Impulssatz und ist die Grundgleichung für die Lösung aller Umströmungsprobleme in einem inkompressiblen Fluid (Luft, Wasser).

* * * * *

9. Nachtrag für eine genauere Rechnung
Die Annahme  konstanter Drücke auf Ober- und Unterseite ist keineswegs zwingend. Da wir eine Anfrage zu diesem Punkt erhalten haben, sei auch die Rechnung angegeben, wenn die Drücke sich linear entsprechend dem Querschnitt bis zur Hinterkante wieder ausgleichen Der Verlauf ist tatsächlich komplizierter und hat schon bei einem Viertel des Wegs von der Vorderkante die Hälfte des Auftriebs aufgebaut; deswegen liefert dieses lineare Modell auch einen geringeren Auftrieb. s sei eine dimensionslose Koordinate mit s =0 an der Vorderkante und s =1 an der Hinterkante. Dann sei mit h ₀= l /2 sin( alfa )

h(s) = h ₀(2 s -1), s im Bereich [0,1]
Q_S = B (l+h ₀ )u ₀= B (l+h(s)) u _1S
Q_D = B (l-h ₀ )u ₀= B (l-h(s)) u _1D
u _1S (s) = u ₀  [ l+h ₀]/[ l+h(s) ]
u _1D (s) = u ₀  [ l-h ₀]/[ l-h(s) ]

Die Berechung ist nun schon etwas länglicher und führt auf den Auftriebsbeiwert c _A   = 8 sin (alfa) / [4-sin (alfa)^2 ]. Für kleine Winkel ist dies Ergebnis c _A   = 2 sin (alfa) und damit die Hälfte des ersten Wertes c _A   = 4 sin (alfa) . Da längs des oberen Weges die Geschwindigkeit immer größer ist als auf der Unterseite, muss sich auch eine Laufzeitdifferenz zwischen den beiden betrachteten Partikeln einstellen.
Man darf nicht erwarten, dass eine solche simple Überlegung das gleiche richtige Ergebnis liefert wie die Lösung der Randwertaufgabe für das Umströmungsproblem dieser Konfiguration " Profil im Windkanal". Wichtig ist uns, dass alle physikalischen Überlegungen auf den gleichen Grundlagen beruhen wie die vollständige Behandlung der Frage nach der Entstehung des Auftriebs.

10. Zirkulation in Theorie und Beobachtung
Es ist bemerkt worden, dass von Zirkulation überhaupt nicht gesprochen wird. Die Zirkulation kann man nicht direkt beobachten. Als Maß für die Wirbeldichte, die eine Fläche normal durchquert, ist sie eine rein theoretische Größe. Für die Erklärung des Auftriebs ist sie auch theoretisch nicht erforderlich; sie kann aber gleichwohl hilfreich sein, weil sie als Integralwert auf kompakte Weise das Maß an Auftrieb kennzeichnet. In der Ausbildung der Sekundarstufe I soll diese Größe nach unserer Auffassung überhaupt nicht verwendet werden. Der wesentliche gedankliche Schritt, der letztlich auf die Zirkulation führt, ist in Bild 1b bereits anschaulich und intuitiv vollzogen worden: die tangentiale Umströmung der Tragfläche mit dem glatten Abfluss an der Hinterkante. Erst die Nachbildung dieses offenkundigen und einsichtigen Vorgangs in einem mathematischen Modell des Windkanals (oder des Freiflugs) schafft den eingangs erwähnten Disput um die Erklärung des Auftriebs.

11. Kann man diesen Ansatz an der Schule überprüfen?
Aus der - in der Tendenz anerkennenden - Stellungnahme eines Hochschuldidaktikers vom 5. März 2003, der als erstes Problem festhält, dass die Bernoullische Gleichung in der Sekundarstufe I nirgendwo in der Bundesrepublik in den Stoffplänen auftritt:

"Ein zweites Problem besteht für mich im Verhältnis zwischen empirischem und theoretischem Vorgehen in der Sekundarstufe I, da der von Ihnen vorgeschlageneStrömungskanal wohl nur in den wenigsten Schulen zur Verfügungsteht und somit die benutzten experimentellen Befunde vor allem geglaubt werden müssten."

Der erste Einwand zur Unterrichtung des Themas ist sehr berechtigt, zumal die ganze Strömungslehre derzeit in den Stoffplänen nicht berücksichtigt wird. Mein Bemühen seit Jahren ist, die Eignung des Themas "Physik des Fliegens" mit seiner Nähe zur Biologie und dem Fliegen in der Natur als Fächer übergreifenden Stoff für die Schule heraus zu stellen. Die Bernoullische Gleichung kann man in der Sekundarstufe I nicht quantitativ behandeln. Aber man kann die Begriffe Druck und Geschwindigkeit einführen und das Prinzip des Manometers erklären. Mit dem "Durchflussexperiment" nach Bernoulli kann man deren Zusammenhang mit dem jeweiligen Querschnitt herstellen, durch den ein fester Volumenstrom fliesst (kleiner Querschnitt:niedriger Druck und große Geschwindigkeit, großer Querschnitt:großer Druck und kleine Geschwindigkeit).
Das zweite genannte Problem ist von uns inzwischen für den Schulunterricht bearbeitet und gelöst worden und ist auf unseren Seiten Spielen und Lernen dokumentiert: In einem Windkanal ist die untere Kanalwand beweglich auf einer Waage gelagert. Im Windkanal befindet sich ein symmetrisches Profil, dessen Anstellwinkel so variiert werden kann, dass Auftrieb und Abtrieb erzielt wird.

• Bei Auftrieb wird die untere Kanalwand nach unten gedrückt und die Waage zeigt eine Belastung an.
• Bei Abtrieb wird die untere Kanalwand angesaugt und die Waage entlastet. Wegen der Symmetrie des Profils ist diese Beobachtung äquivalent zu einer Messung an der oberen Kanalwand bei Auftrieb.

Genau auf dieser Tatsache beruhen ja die voranstehenden Erklärungen. In dem Querschnitt Q_D auf der Druckseite muss sich natürlich auch Überdruck auf dem Kanalboden einstellen. Trotz der beschränkten Messmöglichkeiten bei den niedrigen erzielbaren Geschwindigkeiten (bis ca. 6 m/s) ergibt sich mit dem nachfolgend beschriebenen Versuchsaufbau eine überzeugende Demonstration der voranstehenden Erklärungen.

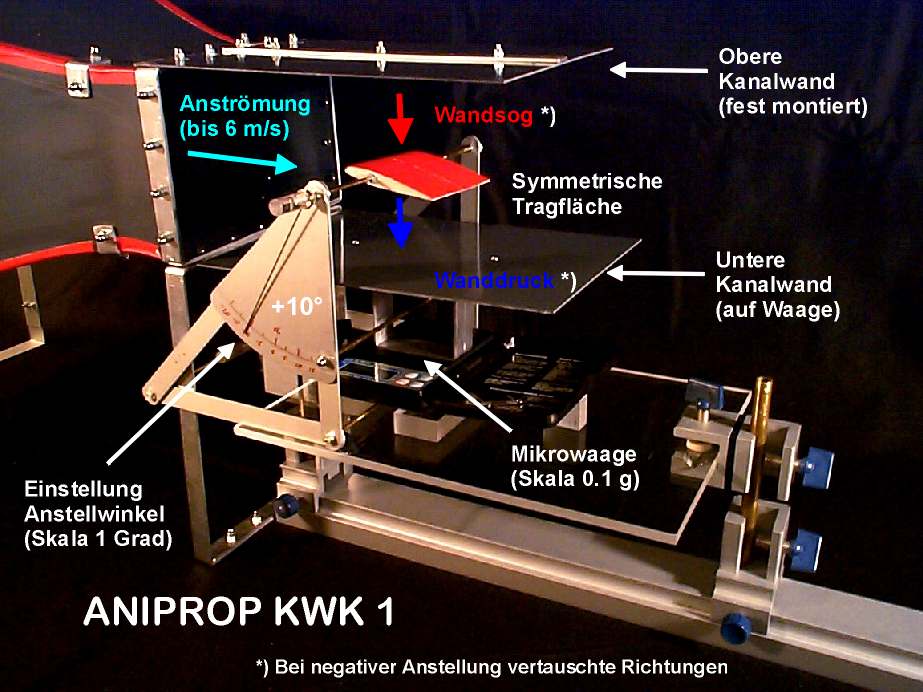Bild 4. Versuchsaufbau zur Messung der Kräfte auf die Wände eines Windkanals.
Mit der Option "Grafik anzeigen"oder einem sinngemäßen Kommando kann das Bild vergrößert dargestellt werden.

Der Querschnitt des Kanals an der Austrittsöffnung beträgt 0.18 x 0.12 m². Die seitlichen Kanalwände sind im Bereich der Messung nicht vorhanden und auch nicht erforderlich. Die Tragfläche hat einen symmetrischen Profilquerschnitt (näherungsweise NACA0012). Die Flügeltiefe beträgt 0.065 m, die Spannweite 0.08 m. Der Kanal lässt sich mit handelsüblichen Bauteilen im Rahmen eines Projektes herstellen. Die Dokumentation auf der Seite Spielen und Lernen wird alle wesentlichen Bauschritte enthalten mit einer Liste der notwendigen Materialien einschließlichder Messgeräte, die allesamt zu erschwinglichen Preisen im Versandhandel verfügbar sind. Die Kräfte entsprechen der Auflage von Massen in der Größenordnung weniger Gramm, wie ein Polarendiagramm mit absoluten Messwerten für ein andere, gewölbte Tragfläche zeigt.

Wer es gleich selbst probieren will: Bei geeignetem Gerät vor Ort kann man diesen Versuch auch mit  jedem vorhandenen Windkanal machen. Man muss dazu auf Höhe des Austrittsortes des Luftstroms eine Bodenplatte unter die Modelltragfläche stellen.Die Bodenplatte muss auf einer Waage aufliegen, die wenigstens 1/10 g anzeigt (eine gewöhnliche Briefwaage ist zu grob).

Die Messbühne ist so gebaut, dass mit der Mikrowaage nacheinander sowohl Auftrieb als auch Widerstand gemessen werden können. Dies zeigen die beiden nachfolgenden Bilder. Die Auflagefläche der Waage ist mit grünem Papier belegt. Der Rahmen, der die Tragfläche hält, belastet die Mikrowaage senkrecht unterhalb der Tragfläche bei der Messung des Auftriebs (Bild 5a). Die Messung des  Widerstands ist möglich, wenn die Kraft über einen Hebel um 90 Grad umgelenkt wird (Bild 5b). Die Halterung für die Tragfläche ruht auf kurzen Rundstäben, so dass die Widerstandskraft praktisch verlustfrei auf die Auflagefläche drückt.
 

Bild 5a. Anordnung zur Messung der Auftriebskraft.	Bild 5b. Anordnung zur Messung der Widerstandskraft.

12. Eine technische Anmerkung
Der voranstehend skizzierte Kanal ist ein Kompromiss zwischen Aufwand und Ergebnis, bei dem nur der Nachweis der Phänomene im Vordergrund steht. Ein Windkanal, in dem zum Beispiel ein Flugmodell von etwa einem Meter Spannweite vermessen werden kann, ist nur in aerodynamischen Labors von Hochschulinstituten und vergleichbaren Forschungseinrichtungen verfügbar.
Aus diesem Grund hat ANIPROP GbR den vergleichsweise preisgünstigen Rundlauf ANIPROP RL3 entwickelt. Von diesem Rundlauf gibt es inzwischen mehrere Kopien, u. a. im Jugendlabor DLR_School_Lab in Göttingen. Dort können nach Absprache jederzeit Versuche mit Flugmodellen durchgeführt werden.