Beiwerte für die ebene Platte 3D

Eine ebene 3D Platte der Flügeltiefe l und der Spannweite b sei gegenüber der Anströmung um den Winkel  angestellt. Die Lösung sei gegeben durch den Vektor  der flächenhaften Wirbeldichte. (x,y) sind flügelfeste Koordinaten, deren Ursprung (0,0) an der Vorderkante der in Anströmung linken Flügelseite liegt. Der hochgestellte Index f ist nachfolgend ausgelassen.

Dann folgt aus der Lösung zunächst das Geschwindigkeitsfeld der Relativbewegung auf Oberseite (+) und Unterseite (-) der Platte:

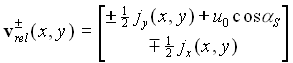
Dieses Geschwindigkeitsfeld geht ein in die Bernoullische Gleichung für den Druckbeiwert:

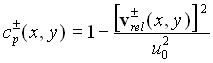
Der örtliche Beiwert der Druckdifferenz  wird durch die Differenz zwischen Unter- und Oberseite bestimmt: . Bei positiver Anstellung ist die Unterseite die Druckseite, die Oberseite die Saugseite. Rechnet man den Beiwert aus den obigen Formeln aus, ergibt sich ein einfacher Zusammenhang:

.

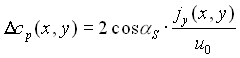Für eine bestimmte Spannweite y ergibt sich der örtliche Beiwert der Normalkraft (Kraft senkrecht auf der Plattenebene) durch Integration über die Flügeltiefe:

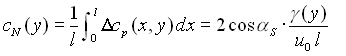mit 

ist die örtliche Zirkulation. Ihr Wert ist in der Symmetrieebene des Flügels am größten, wo alle Wirbeldichte quer zur Anströmung gerichtet ist. Betrachtet man die Komponente  der Wirbeldichte an der Hinterkante xH, so gilt
 . Die Gesamtzirkulation ist stets null. Die größte Zirkulation ergibt sich bei halber Spannweite. Der Normalkraftbeiwert für die ganze Platte ergibt sich dann als

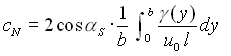
Der Zusammenhang zwischen den Beiwerten von Normalkraft FN und Auftriebskraft FA lautet . Der induzierte Widerstandsbeiwert ist .

Anmerkung: Die leistungsfreie 2D Strömung () erhält man mit voran stehender Rechnung nur, wenn man die ebene Platte als Grenzfall eines immer dünneren Profils behandelt (da sonst die Umströmung der Vorderkante nicht ganz korrekt erfasst wird).

14.06.2013 Berichtigung nicht angezeigter Formeln.